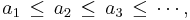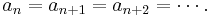Ascending chain condition

The ascending chain condition (ACC) and descending chain condition (DCC) are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings.^[1]^[2]^[3] These conditions played an important role in the development of the structure theory of commutative rings in the works of David Hilbert, Emmy Noether, and Emil Artin. The conditions themselves can be stated in an abstract form, so that they make sense for any partially ordered set. This point of view is useful in abstract algebraic dimension theory due to Gabriel and Rentschler.

1 Definition
- 1.1 Comments
2 See also
3 Notes
4 References

Definition

A partially ordered set (poset) P is said to satisfy the ascending chain condition (ACC) if every ascending chain of elements eventually terminates. Equivalently, given any sequence of elements of P

$a_1 \,\leq\, a_2 \,\leq\, a_3 \,\leq\, \cdots,$

there exists a positive integer n such that

$a_n = a_{n%2B1} = a_{n%2B2} = \cdots.$

Similarly, P is said to satisfy the descending chain condition (DCC) if every descending chain of elements eventually terminates, or equivalently if any descending sequence

$\cdots \,\leq\, a_3 \,\leq\, a_2 \,\leq\, a_1$

of elements of P eventually stabilizes (that is, there is no infinite descending chain).

Comments

A subtly different and stronger condition than "containing no infinite ascending/descending chains" is "contains no arbitrarily long ascending/descending chains (optionally, 'based at a given element')". For instance, the disjoint union of the posets {0}, {0,1}, {0,1,2}, etc., satisfies both the ACC and the DCC, but has arbitrarily long chains. If one further identifies the 0 in all of these sets, then every chain is finite, but there are arbitrarily long chains based at 0.

The descending chain condition on P is equivalent to P being well-founded: every nonempty subset of P has a minimal element (also called the minimal condition).

Similarly, the ascending chain condition is equivalent to P being converse well-founded: every nonempty subset of P has a maximal element (the maximal condition).

Every finite poset satisfies both ACC and DCC.

A totally ordered set that satisfies the descending chain condition is called a well-ordered set.

Notes

^ Hazewinkel, Gubareni & Kirichenko (2004), p.6, Prop. 1.1.4.
^ Fraleigh & Katz (1967), p. 366, Lemma 7.1
^ Jacobson (2009), p. 142 and 147

References

Atiyah, M. F., and I. G. MacDonald, Introduction to Commutative Algebra, Perseus Books, 1969, ISBN 0-201-00361-9
Michiel Hazewinkel, Nadiya Gubareni, V. V. Kirichenko. Algebras, rings and modules. Kluwer Academic Publishers, 2004. ISBN 1-4020-2690-0
John B. Fraleigh, Victor J. Katz. A first course in abstract algebra. Addison-Wesley Publishing Company. 5 ed., 1967. ISBN 0-201-53467-3
Nathan Jacobson. Basic Algebra I. Dover, 2009. ISBN 978-0-486-47189-1

Ascending chain condition

Contents

Definition

Comments

See also

Notes

References